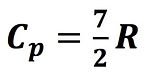Specific Heats
When the temperature of a material increases from T to T + dT, due to a small amount of heat dq being added to the unit mass of material, without any change in phase occuring within the material, the ratio dq/dT is called the specific heat of the material.
More simply: Specific heat is the amount of heat needed to raise the temperature of one gram (g) of a substance by one degree celcius (C).
Heating 1 g of a liquid would take about 1 calorie to raise its temperature by 1 degree C. So water therefore has a specifc heat of 1. However, putting the same mass of dry soil on the same flame as the liquid we would see it would only take 1/5th of the heat to raise the temperature by 1 degree C. Therefore the specific heat of water is 5 times greater than that of soil. This means the water must absorb 5 times more heat as the same quantity of soil in order to increase its temperature by the same amount.
As well as heating slowly, water also cools slowly, having a much higher capacity for heat storage than other substances. A certain amount of water can store large amounts of energy while undergoing only a small temperatyre change. It is because of this that water has a large influence on the weather and climate. Areas near bodies of water such as lakes or oceans will expericence warmer winters and cooler summers because of this, compared to nearby areas inland/away from water.
Depending on how the material changes as it recieves the heat the specific heat could have any number of values. One option is to keep the volume of the material constant.
A specific heat at constant volume Cv is defined as:
Another option is to keep the pressure of the material constant.
A specific heat at constant pressure is defined as:
The specific heat at constant volume, Cv, is 717 J K^-1 kg^-1
The specific heat at constant pressure is 1004.5 J K^-1 kg^-1
The difference between them is R, the gas constant for dry air: 287 J K^-1 kg^-
Statistical methods reveal that Cv and Cp are related to R. For example, diatomic molecules.