The First Law of Thermodynamics
The First Law of Thermodynamics states: The change in the internal energy of a system is equal to the heat added to the system minus the work done by the system.
It expresses the principle of conservation of energy, ie, energy cannot be created or destroyed, it can only change form. In other words, any energy lost during one process must equal the energy gained by another. Hence the total energy in a closed system (no exchange of mass) is constant.
A change in temperature or internal energy of a gas can be achieved in two ways:
1) By adding or subtracting heat
2) By compression or expansion, ie, doing work
As well as the kinetic and potential energy that a system as a whole may possess, it also contains internal energy due to the kinetic and potential energy of its molecules or atoms. Increases in the internal kinetic energy, ie, molecular motions, are manifested as an increase in the temperature of the system. Changes in the potential energy of the molecules are caused by any changes in their relative positions, due to any forces acting between the molecules.
Let us suppose at a closed system of unit mass takes in a certain quantity of thermal energy q (measured in joules), which it can recieve by thermal conduction and/or radiation. As a result the system may do a certain amount of external work w (also measured in joules). The excess of the energy supplied to the body over and above the external work done by the body is q - w. Therefore, if there is no change in the macroscopic kinetic and potential energy of the body, it follows from the principle of conservation of energy that the internal energy of the system must increase by q - w. That is:
q -w = usub2 - usub1 (1)
where usub2 and usub1 are the internal energies of the system before and after the change. In differential form (1) becomes:
dq - dq = du (2)
where dq is the differential increment of heat added to the system, dw is the differential element of work done by the system and du is the differential increase in the internal energy of the system,
Equations (1) and (2) are statements of the first law of thermodynamics. (2) provides a deffinition of du. The change in internal energy of du depends only on the initial and final states of the system and is therefore independant of the maner by which the system is transferred between these two states. This parameter is referred to as a funtion of state.
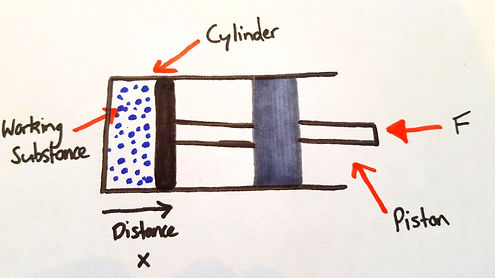
To visualise the work term dw in (2) in a simple case, consider a substance, usually called the working substance, contained in a cyclinder of fixed cross-sectional area that is fitted with a movable, frictionless piston (Figure. 1)
The volume of the substance is proportional to the distance from the base of the cylinder to the face of the piston and can be represented on the horizontal axis of the graph shown in Figure. 1. The pressure of the substance in the cyclinder can be represented on the vertical axis of this graph. Therefore, every state of the substance, corresponding to a given position, is represented by a point of the p - V diagram. When the substance is in equilibrium at a state represeted by a point P on the graph, its pressure is p and its volume is V. If the piston moves outward through an incremental distance dx while its pressure remains essentially constant at p, the work dW done by the substance in pushing the external force F through a distance dx is:
dW = Fdx
or, because F = pA where A is the cross sectional area of the face of the piston,
dW = pA dx = pdV (3)
The work done by the substance when its volume increases by a small increment dV is equal to the pressure of the substance multiplied by its increase in volume, which is equal to the blue-shaded area in the graph (Figure 1), which is equal to the area under the curve PQ.
When a substance moves from state A with Volume V1 to state B with volume V2, during which its pressure changes, the work done W by the material is equal to the area under the curve AB:
W = pdV (4)
Equation (3) and (4) are fairly general and represent work done by any substance or system, due to a change in its volume.
If V2 > V1, W is positive, indicating that the substance does work on its environment.
If V2 < V1, W is negative, which indicates that the environment does work on the substance.
When dealing with a unit mass of a substance, the volume V is replaced by the specific volume .
Therefore, dw, the work that is one when the specific volume increases by d is:
dw = pd (5)
Combining (2) and (5):
dq = du + p d
an alternative form of the 1st Law.
Other forms of the 1st Law:
Figure 1. Representation of the state of a working substance in a cyclinder on a pressure - Volume diagram. Theblue shaded area above 'V' is equal to p dV, which is the work done by the working substance in passing from P to Q.
V2
V1

In the atmosphere most processes occur with negligible changes in Q. When dQ = 0 a process is called adiabatic.
The first Law becomes: dQ = CpdT - (RT/p)dp = 0 (see derivation below)
ø = the potential temperature. This is the temperature that an air parcel would have if brought adiabatically to pressure p0.
ø is conserved for adiabatic processes. I.e.air parcels tend to follow ø surfaces.
In the atmosphere processes do not usually occur at constant volume, however they can occur at constant pressure.